Views > Financial modeling > Avoid circularity in financial models

Dogbert: I plan to open a gambling casino for people who have extraordinarily bad luck.
Dilbert: How can you tell who has extraordinarily bad luck?
Dogbert: They would be the ones that go to my casino.

Dilbert by Scott Adams

Many finance problems inherently involve circular calculations. The most common of them is balancing the balance sheet. We all know that Assets should always equal Liabilities and Stockholder's Equity, don't we? But in order to prepare the balance sheet we need to prepare the income statement—since retained earnings should be carried to the balance sheet from the income statement. At the same time, without the balance sheet being ready, we can't figure out the interest expense associated with the amount of external financing—an item required to prepare the income statement. So how do we typically solve such kind of modeling problems?

There are four basic approaches to handle circular calculations in Excel:

Deliberate use of circular references
Goal seek/VBA macros
Algebraic (closed-form) solutions
Manual iterations (trial and error)

The first two techniques are somewhat risky and inefficient, the third is rarely practical in real world scenarios and the fourth is recommended.

DELIBERATE USE OF CIRCULAR REFERENCES
Circular references are usually considered by experts a bad thing to have in a spreadsheet model. The FAST standard—published by the FAST Standard Organization, a nonprofit promoting standardization in financial modeling—article 1.01-11 states clearly to “Never release a model with purposeful use of circularity”. The drawbacks of circular references are very well documented in Jonathan Swan's Practical Financial Modeling, A Guide to Current Practice—another authority on the use of spreadsheets as a financial analysis tool—and summarized here:

Inefficiency. They can be very memory intensive, as Excel will trigger recalculation of all the dependent worksheets—on each iteration—every time something changes in the model.
Risk. Once you enable iterations to allow Excel to calculate deliberate circular references, it becomes very difficult to distinguish between “mistakes” that have created inadvertent circular references and the intentional circular reference—since Excel won't warn you about the existence of such circular references.

GOAL SEEK / VBA MACROS
Goal seek and VBA macros are extremely powerful tools in Excel. However, they are considered static procedures—if the inputs change, the procedures have to be repeated. Therefore, their use to solve circularity problems will put the user at the mercy of his/her memory to remember when to execute the macro or initiate the goal seek procedure. How often have you found yourself tweaking the assumptions of a model to finally reach satisfactory results, but then to belatedly realize that you haven't pressed that macro button that will initiate the calculations to converge the results to the right solution—invalidating all the trials you were trying to do? But wait, it happens to the best of us.

ALGEBRAIC (CLOSED-FORM) SOLUTIONS
Closed form solutions are probably the most elegant of all four techniques, but they aren't possible in most practical cases—where finding a solution to an algebraic expression relating many variables over a large number of time periods is simply impossible without iterations.

MANUAL ITERATIONS (TRIAL AND ERROR)
The manual iterations technique entails solving the circularity problem by computing successive approximations to the solution starting from an initial guess. The Excel implementation of such iterative solutions involves building manually—hence the name of the technique—blocks of calculations that will ultimately converge to the solution within an acceptable margin of error. However, once implemented, the methodology becomes completely automatic and doesn't require the intervention of the user.

The beauty of the manual iterations technique is its similarity with Circular References of Excel—in the sense that it's iterative and automatic—but without the drawbacks of Circular References as explained above. Moreover, being automatic makes the technique superior to the Goal seek/Macro methodology—that requires manual intervention of the user with every change in the inputs.

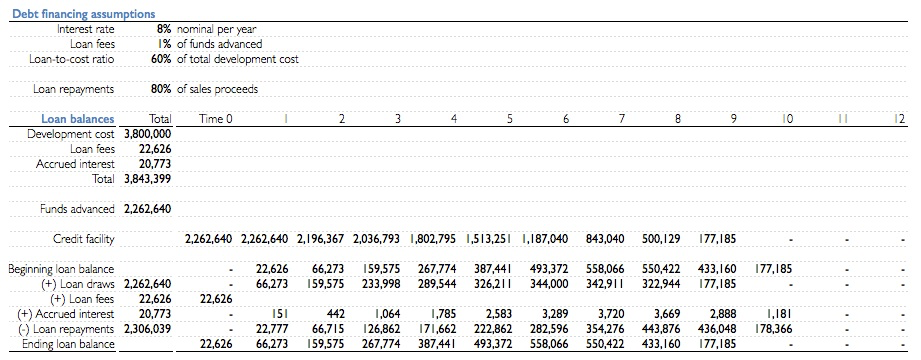
Lets take an example to describe the methodology. Suppose a real estate developer is planning to build a condominium on a piece of land that was just bought for $1,000,000. On top of that, the developer budgeted a total of $2,800,000 to build all the site improvements including the building. In return, the developer expects to sell the apartments for a total net sale—after deducting all expenses—of $6,400,000. The total building and selling of the project is expected to take 12 months. The table below summarizes the projected monthly draws to pay the construction costs along with the net sales proceeds.

The developer obtained a commitment from a construction lender to partially finance the construction costs. Given the market conditions in the debt markets the terms of the construction loan are as follows:

Interest rate = 8% (nominal per year)
Loan fees = 1% of funds advanced paid at closing
Loan-to-Cost ratio = 60% of total development cost
Loan repayment = 80% of sale proceeds

The loan fees and interest expense are added to the loan balance so that the developer doesn't have to make out-of-pocket payments after closing on the land. The developer files draw requests with the construction lender each month as work progresses on the project. The lender funds the request by transferring money into the developer's project account. This money is then available for the developer to pay the contractor. Since the construction lender will only finance 60 percent of the total development cost, the developer is expected to fill any gap in funding construction by sales of the individual units that make up the project. The agreement entails the developer to pay 80 percent of the net sales proceeds on the sale of each unit to the lender to payback the construction loan.

As you can see from the table below, the total development cost is $3,843,399 and the funds advanced amount to $2,262,640. The loan fees and accrued interest—which are a very real part of the development cost—are respectively $22,626 and $20,773. The loan amount is $2,306,039 ($2,262,640 + $22,626 + $20,773)—implying a Loan-to-Cost ratio of exactly 60%. The construction loan is paid down completely in month 10.

Now the pressing question is how did we know that the lender should only advance $2,262,640 so that the loan amount—including interest and fees—equals $2,306,039 or 60 percent of the total development cost?

Given that:

The loan amount depends on the total development cost.
The total development cost depends on the loan fees and accrued interest.
The loan fees and accrued interest depend on the loan amount.

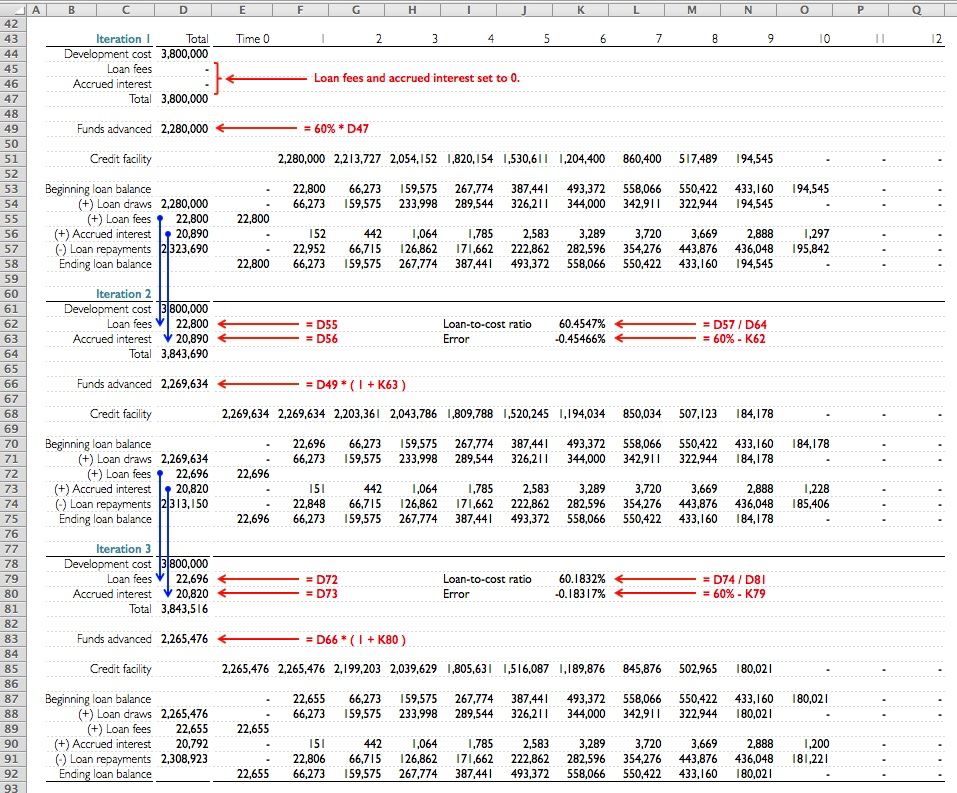
Well the answer to that is Manual Iterations. It is a systematic way of repeating the Loan balances block of calculations—as shown in the table above—a finite number of steps to reach a solution. To explain the methodology look at the table below that shows the first three iterations—out of a sequence of 20 approximations—that we've used to converge to almost the exact solution within an acceptable margin of error.

Step1: We start the process by taking an initial guess at the final solution. In iteration 1 we assumed Loan fees and Accrued interest equal to zero. The resulting total development cost is $3,800,000. We also start iteration 1 by assuming that Funds advanced equals to 60% (loan-to-cost ratio) of $3,800,000—that is $2,280,000. As you can see the calculations result in Loan fees = $22,800 and Accrued interest = $20,890—cells D55 and D56 respectively. The resulting Loan amount (cell D57) equals to $2,323,690—off by $17,651 from $2,306,039.

Step 2: Substitute the calculated values for Loan fees and Accrued interest into the respective cells of iteration 2. This results in a revised total development cost of $3,843,690. Then, calculate the new loan-to-cost ratio (cell K62) along with a margin of error (cell K63)—60.4547% and -0.45466% respectively. Finally adjust the Funds advanced in iteration 2 by multiplying the Funds advanced from iteration 1 by the factor (1 + Error). The new Funds advanced equals to $2,269,634 and the resulting Loan amount is $2,313,150—off by $7,111 from $2,306,039.

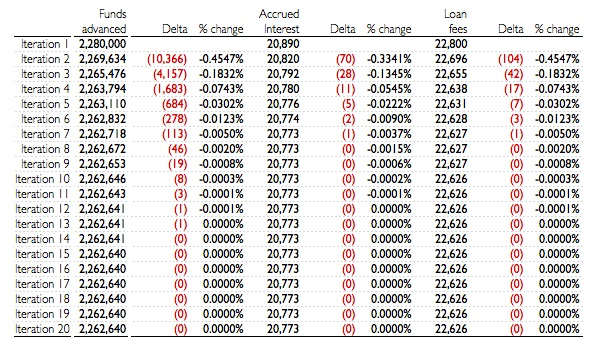
Step 3, 4, 5…20: Continue substituting Loan fees and Accrued interest into the respective cells and refining Funds advanced from preceding iterations by the (1 + Error) factor and watch for them to converge to final values.

As you can see from the table below, that after 12 iterations, the Funds advanced converges to $2,262,641 with an approximate error estimate of $1 or 0.0001%.

AVOID CIRCULARITY IN FINANCIAL MODELS

We showed you four different techniques that could be used to solve circular problems and explained in details the mechanics of the Manual Iteration technique. We highly recommend this methodology for the following reasons:

It's automatic and not static—eliminates user interference.
It eliminates the risk of errors that are usually associated with Circular References.
It's efficient and not volatile—enhances calculation time.